FRACCIONES

¿Qué es una fracción?

La Fracción o número fraccionario es la expresión matemática de una cantidad determinada de porciones que se toman de un «todo» dividido en partes iguales; es decir, la fracción es una parte de una total.

Veamos el siguiente gráfico:

Este círculo ha sido dividido en cuatro partes iguales. Entonces decimos que cada porción representa a una fracción.

Sean: a y b elementos de una fracción, entonces la fracción es la división de «a ÷ b» y su representación matemática es:

$\dpi{150} \large \mathbf{\frac{a}{b}}$

Además, para que esta expresión sea una fracción se debe cumplir que:

«a» y «b» sean números enteros (ℤ).
Al dividir «a» entre « b» el resultado no debe ser exacto.

Ejemplos:

Luego de ver la definición de fracciones podemos mencionar algunos ejemplos:

$\large \frac{1}{2}; \frac{6}{13}; \frac{4}{5}; \frac{1}{7}; \frac{3}{11}; \frac{5}{6}; \frac{5}{3}; \frac{7}{9}; \frac{3}{8};\frac{23}{27}$

Partes de una Fracción

Una fracción tiene tres partes, para conocerlos observe la siguiente figura:

Línea fraccionaria: Toda fracción tiene una línea horizontal que separa el numerador del denominador.
Numerador: Es el número que está arriba de la línea fraccionaria, indica el número de partes que se toman de la unidad.
Denominador: Es el número que está en la parte inferior de la línea fraccionaria, indica el número de partes iguales en que se divide la unidad.

¿Cómo se lee una fracción?

Sabemos que el denominador representa cuantas partes iguales se divide la unidad; en ese sentido, podemos decir que cuando la unidad se divide en 2 partes iguales, cada una de esas partes se llama medio. Cuando la unidad se divide en 5 partes iguales, cada parte se le llama quinto.

Entonces, veamos cómo se leen las fracciones de acuerdo al valor que tenga el denominador:

2: medio
3: tercios
4: cuarto
5: quintos
6: sextos
7: séptimos
8: octavos
9: novenos
10: décimos
11: onceavos
12: doceavos
…

Cuando se lee una fracción, primero se menciona al númerador y luego al denominador. En caso del numerador, este toma el nombre tal cual se le conoce. Vea un ejemplo:

$\large \mathbf{\frac{{\color{Blue} 2}}{{\color{Red} 3}}:}$ Se lee: «dos tercios«

¿Qué significa?: Significa que se han tomado 2 de partes, después después de haber dividido la unidad en tres partes iguales.

Ejemplos:

a. $\large \mathbf{\frac{1}{2}:}$ un medio

b. $\large \mathbf{\frac{1}{10}:}$ un décimo

c. $\large \mathbf{\frac{7}{5}:}$ siete quintos

d. $\large \mathbf{\frac{2}{9}:}$ dos novenos

e. $\large \mathbf{\frac{11}{23}:}$ once veintitresavos

Clasificación de fracciones

Fracciones propias

Se llaman fracciones propias a aquellas que representan números menores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número menor que la unidad se caracterizan por tener el numerador menor que el denominador. Por ejemplo:

$clasificación de fracciones 1$

Fracciones impropias

Se llaman fracciones impropias a las que representan números mayores que la unidad. Y ¿cómo son estas fracciones? Todas las fracciones que representan un número mayor que la unidad se caracterizan por tener el numerador mayor que el denominador. Por ejemplo:

$clasificación de fracciones 2$

Fracciones iguales a la unidad

Son las que representan números iguales a la unidad. Es decir, son las fracciones que representan el 1 y se caracterizan por tener el numerador y el denominador iguales.

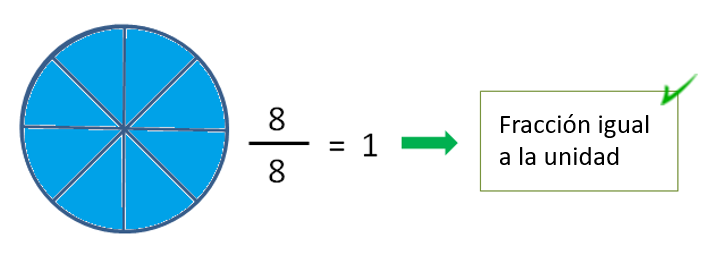
$clasificación de fracciones$

Ejemplos de clasificación de fracciones

Vamos a ver ejemplos clasificando estas fracciones:

2527; 12; 54 ; 180180 ; 363 ; 66 ; 42 ; 1010; 200279

2527 < 1 ya que el numerador es menor que el denominador: Es una fracción propia

12 < 1 ya que el numerador es menor que el denominador: Es una fracción propia

54 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia

180180 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad

363 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia

66 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad

42 > 1 ya que el numerador es mayor que el denominador: Es una fracción impropia

1010 = 1 ya que el numerador es igual al denominador: Es una fracción igual a la unidad

200279 < 1 ya que el numerador es menor que el denominador: Es una fracción propia

Expresión Gráfica de una Fracción

Una fracción puede expresarse gráficamente siempre y cuando las partes de un todo sean iguales, veamos 3 ejemplos:

Ejemplo 01:

Aquí tenemos un ejemplo sencillo de fracciones.

Un todo ha sido dividido en dos partes iguales; por lo

que el denominador sería 2. La sección sombrada de la imagen es sólo la mitad, esto se representa en fracción como «un medio«, así:

$\large \mathbf{\frac{1}{2}}$

Así mismo; la imagen sin sombrear también será representado por la fracción:

$\large \mathbf{\frac{1}{2}}$

Buscar este blog

bloggcaratula

FRACCIONES

FRACCIONES

¿Qué es una fracción?

Ejemplos:

Partes de una Fracción

¿Cómo se lee una fracción?

Ejemplos:

Clasificación de fracciones

Fracciones propias

Fracciones impropias

Fracciones iguales a la unidad

Ejemplos de clasificación de fracciones

Expresión Gráfica de una Fracción

Ejemplo 01:

Comentarios

Publicar un comentario

Entradas más populares de este blog

fotosíntesis